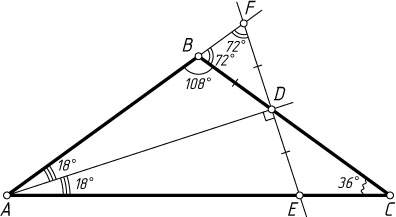
1183. Угол при вершине B
равнобедренного треугольника ABC
равен 108^{\circ}
. Перпендикуляр к биссектрисе AD
этого треугольника, проходящий через точку D
, пересекает сторону AC
в точке E
. Докажите, что DE=BD
.
Указание. Пусть указанный перпендикуляр пересекает прямую AB
в точке F
. Докажите, что треугольники AFE
и BDF
— равнобедренные.
Решение. Пусть указанный перпендикуляр пересекает прямую AB
в точке F
. Тогда высота AD
треугольника AFE
является его биссектрисой, поэтому DF=DE
. Поскольку
\angle FBD=180^{\circ}-108^{\circ}=72^{\circ}~\mbox{и}~\angle AFD=90^{\circ}-18^{\circ}=72^{\circ},
то треугольник BDF
— равнобедренный. Следовательно, BD=DF=DE
.