11883. В треугольник ABC
вписан квадрат площади 36 со стороной на отрезке AB
(см. рис.). В каждый из двух образовавшихся при этом прямоугольных треугольников вписан квадрат, имеющий со своим треугольником общий прямой угол. Площади квадратов равны 4 и 9. Найдите площадь треугольника ABC
.
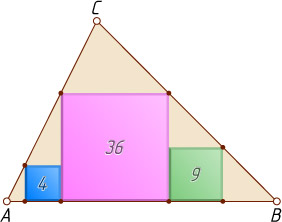
Ответ. 75.
Решение. Стороны квадратов равны 2, 6 и 3. Применив подобие и теорему о средней линии треугольника, найдём, что крайние отрезки стороны AB
равны 1 и 3, поэтому
AB=1+2+6+3+3=15.
Пусть высота треугольника ABC
, проведённая из вершины C
, равна h
. Из подобия получаем \frac{h-6}{h}=\frac{6}{15}
, откуда h=10
. Следовательно,
S_{\triangle ABC}=\frac{1}{2}AB\cdot h=\frac{1}{2}\cdot15\cdot10=75.
