1190. На стороне AB
квадрата ABCD
построен равносторонний треугольник ABM
. Найдите угол DMC
.
Ответ. 30^{\circ}
или 150^{\circ}
.
Указание. Найдите углы равнобедренного треугольника DAM
.
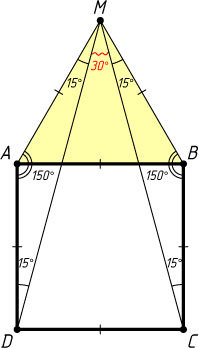
Решение. Пусть точка M
расположена вне квадрата ABCD
(рис. 1). Тогда угол при вершине A
равнобедренного треугольника DAM
равен 90^{\circ}+60^{\circ}=150^{\circ}
, поэтому
\angle AMD=\frac{180^{\circ}-150^{\circ}}{2}=15^{\circ}.
Аналогично находим, что \angle BMC=15^{\circ}
. Следовательно,
\angle DMC=60^{\circ}-15^{\circ}-15^{\circ}=30^{\circ}.
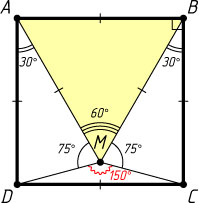
Если точка M
расположена внутри данного квадрата (рис. 2), то аналогично находим, что \angle DMC=150^{\circ}
.