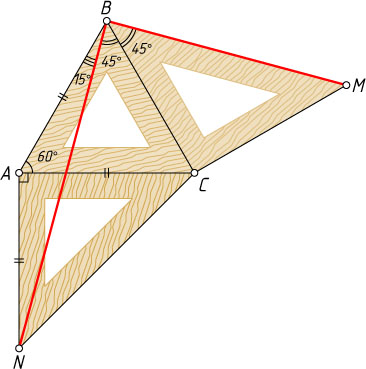
1191. На сторонах AC
и BC
равностороннего треугольника ABC
построены внешним образом равнобедренные прямоугольные треугольники ACN
и BCM
с прямыми углами при вершинах A
и C
соответственно. Докажите, что BM\perp BN
.
Указание. Вычислите углы ABN
и CBN
.
Решение. Треугольник BAN
равнобедренный, так как AB=AC=AN
. Поскольку
\angle BAN=\angle BAC+\angle CAN=60^{\circ}+90^{\circ}=150^{\circ},
\angle ABN=\frac{180^{\circ}-\angle BAN}{2}=\frac{180^{\circ}-150^{\circ}}{2}=15^{\circ},
поэтому
\angle CBN=\angle CBA-\angle ABN=60^{\circ}-15^{\circ}=45^{\circ}.
Следовательно,
\angle MBN=\angle CBN+\angle CBM=45^{\circ}+45^{\circ}=90^{\circ}.