11974. Даны два прямоугольника ABCD
и DEFG
, причём точка E
лежит на отрезке AD
, точка G
лежит на отрезке CD
, а точка F
— центр вписанной окружности треугольника ABC
(см. рис.). Во сколько раз площадь прямоугольника ABCD
больше площади прямоугольника DEFG
?
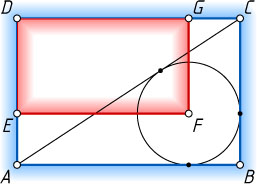
Ответ. 2.
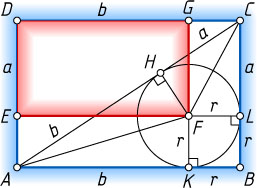
Решение. Первый способ. Пусть вписанная окружность радиуса r
прямоугольного треугольника ABC
касается катетов AB
и BC
в точках K
и L
соответственно, а гипотенузы AC
— в точке H
. Обозначим CH=CL=DE=a
и AH=AK=DG=b
. Тогда равны прямоугольные треугольники CHF
и CLF
, прямоугольные треугольники AHF
и AKF
, а BKFL
— квадрат со стороной r
. Значит,
S_{ABCD}=AB\cdot BC=(AK+KB)(CL+LB)=(b+r)(a+r)=
=(a+b)r+ab+r^{2}=ab+((a+b)r+r^{2})=DE\cdot DG+AC\cdot FH+FL^{2}=
=S_{DEFG}+2S_{\triangle ACF}+S_{BKFL}=S_{DEFG}+S_{\triangle ABC}=S_{DEFG}+\frac{1}{2}S_{ABCD},
откуда S_{ABCD}=2S_{DEFG}
.
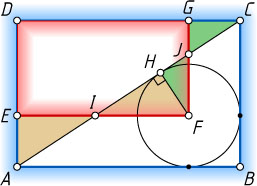
Второй способ. Пусть диагональ AC
прямоугольника ABCD
пересекает отрезки EF
и FG
в точках I
и J
соответственно. Высота FH
треугольника FIJ
равна радиусу данной окружности, а значит, равна отрезкам AE
и GC
. Тогда прямоугольные треугольники FHI
и AEI
равны по катету и противолежащему острому углу. Аналогично, равны треугольники FHJ
и CGJ
. Тогда площадь прямоугольника DEFG
равна площади треугольника ACD
, а это половина прямоугольника ABCD
.
Автор: Андреева А. Н.
Автор: Панов М. Ю.
Источник: Журнал «Квант». — 2020, № 11-12, с. 31, задача 14
Источник: Летний турнир им. А. П. Савина «Математика 6—8». — 2020, № 14


