11982. Даны пересекающиеся окружности \Gamma_{1}
и \Gamma_{2}
с центрами O_{1}
, O_{2}
и радиусами R\gt r
соответственно. Через точку P
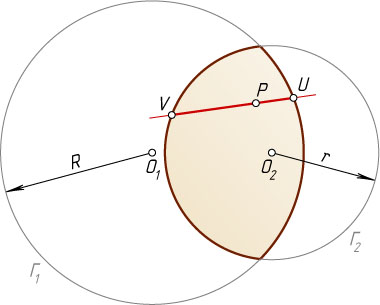
, лежащую внутри выпуклой фигуры, ограниченной этими окружностями, проводятся прямые, пересекающие первую окружность в точке U
, а вторую — в точке V
, как показано на рисунке. Через точку P
проведите прямую, для которой произведение PU\cdot PV
принимает наименьшее значение.
Ответ. Искомая прямая проходит через внешний центр гомотетии данных окружностей.
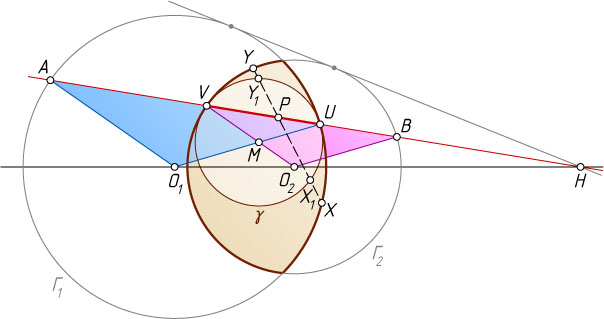
Решение. Пусть H
— внешний центр гомотетии данных окружностей (точка пересечения их общей касательной и линии центров). Докажем, что искомая прямая — это прямая PH
.
Пусть U
и V
— точки пересечения границы указанной в условии фигуры с прямой PH
(точка U
на дуге окружности \Gamma_{1}
, а точка V
на дуге окружности \Gamma_{2}
), точки A
и B
— вторые точки пересечения прямой PH
с \Gamma_{1}
и \Gamma_{2}
соответственно, M
— точка пересечения O_{1}U
и O_{2}V
.
Из гомотетии следует, что O_{2}B\parallel O_{1}U
и O_{2}V\parallel O_{1}A
, а так как треугольники BO_{2}V
и UO_{1}A
равнобедренные, то подобный им треугольник UMV
тоже равнобедренный, MU=MV
.
Окружность \gamma_{1}
с центром M
и радиусом MU
внутренним образом касается окружности \Gamma_{1}
, так как расстояние между центрами эти окружностей равно разности их радиусов. Аналогично, окружность \gamma_{2}
с центром M
и радиусом MV
внутренним образом касается окружности \Gamma_{2}
, а так как MU=MV
, то окружности \gamma_{1}
и \gamma_{2}
— это одна и та же окружность. Обозначим её \gamma
.
Окружность \gamma
расположена внутри окружности \Gamma_{1}
и внутри окружности \Gamma_{2}
, поэтому любая отличная от PH
прямая, проходящая через точку P
, высекает из рассматриваемой фигуры хорду XY
, для которой PX\cdot PY\geqslant PU\cdot PV
(если X_{1}
и Y_{1}
— точки пересечения прямой XY
с \gamma
, лежащие на лучах PX
и PY
соответственно, то PX\geqslant PX_{1}
и PY\geqslant PY_{1}
, а при этом PX_{1}\cdot PY_{1}=PU\cdot PV
).
Источник: Журнал «Crux Mathematicorum». — 1982, № 7, задача 656, с. 211

