1204. Теорема Вариньона. Докажите, что середины сторон любого четырёхугольника являются вершинами параллелограмма.
Указание. Примените свойство средней линии треугольника.
Решение. Пусть M
, N
, K
, L
— середины сторон соответственно AB
, BC
, CD
, AD
четырёхугольника ABCD
. Поскольку MN
— средняя линия треугольника ABC
, то MN=\frac{1}{2}AC
и MN\parallel AC
. Аналогично докажем, что KL=\frac{1}{2}AC
и KL\parallel AC
. Значит, MN=KL
и MN\parallel KL
. Следовательно, четырёхугольник MNKL
— параллелограмм.
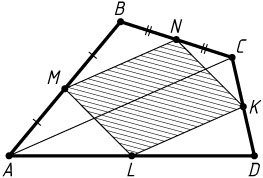
Примечание. Площадь этого параллелограмма равна половине площади исходного четырёхугольника.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 36, с. 64
Источник: Яглом И. М. Геометрические преобразования. — Т. 1: Движения и преобразования подобия. — М.: ГИТТЛ, 1955. — № 14(а), с. 31
Источник: Погорелов А. В. Геометрия: Учебное пособие для 7—11 кл. средней школы. — 8-е изд. — М.: Просвещение, 1989. — № 47
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — с. 67
Источник: Шарыгин И. Ф. Геометрия 7—9: Учебник для общеобразовательных учебных заведений. — М.: Дрофа, 2002. — № 2, с. 157
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 20
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.2, с. 12
