12068. Окружности с центрами O
и O'
расположены на плоскости одна вне другой. Касательная, проведённая из точки O
ко второй окружности, пересекает первую окружность в точках A
и B
, а касательная из O'
к первой окружности пересекает вторую окружность в точке в точках A'
и B'
, причём точки A
и A'
лежат по одну сторону от прямой OO'
. Зная расстояния AA'=a
и BB'=b
, найдите OO'
.
Ответ. \frac{a+b}{2}
.
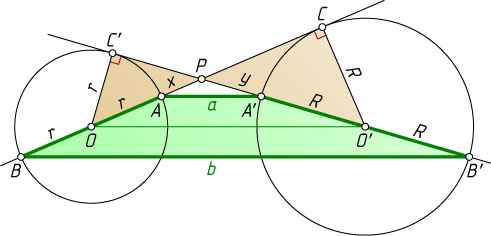
Решение. Рассмотрим случай, изображённый на рисунке.
Пусть прямые AB
и A'B'
пересекаются в точке P
, прямая AB
касается второй окружности радиуса R
в точке C
, а прямая A'B'
касается первой окружности радиуса r
в точке C'
. Обозначим PA=x
, PA'=y
.
Из подобия прямоугольных треугольников OC'P
и O'CP
получаем
\frac{OP}{OC'}=\frac{O'P}{O'C}~\Rightarrow~\frac{x+r}{r}=\frac{y+R}{R}~\Rightarrow~\frac{x}{r}+1=\frac{y}{R}+1~\Rightarrow
\Rightarrow~\frac{x}{r}=\frac{y}{R}~\Rightarrow~\frac{PA}{AO}=\frac{PA'}{A'O}~\Rightarrow~AA'\parallel OO';
\frac{PA}{AB}=\frac{x}{2r}=\frac{y}{2R}=\frac{PA'}{A'B'}~\Rightarrow~AA'\parallel BB'.
Значит, OO'\parallel AA'\parallel BB'
, т. е. ABB'A'
— трапеция с основаниями AA'=a
и BB'=b
, а OO'
— её средняя линия. Следовательно,
OO'=\frac{AA'+BB'}{2}=\frac{a+b}{2}.
Источник: Международная олимпиада «Интеллектуальный марафон». — 1994, IV, задача 5
Источник: Журнал «Квант». — 1995, № 2, с. 56, задача 5
