12087. Дан прямоугольный треугольник ABC
с прямым углом C
. Прямая, проходящая через середину его высоты CH
и вершину A
, пересекает CB
в точке K
. Пусть L
— середина BC
, а T
— точка на отрезке AB
, для которой \angle ATK=\angle LTB
. Известно, что BC=1
. Найдите периметр треугольника KTL
.
Ответ. 1.
Решение. Пусть E
— середина CH
, а точки M
и N
симметричны точке L
относительно прямых AB
и AC
соответственно. Тогда AM=AL=AN
и \angle MAN=2\angle BAC
.
Прямоугольные треугольники ABC
и ACH
с общим острым углом при вершине A
подобны, отрезки AE
и AL
— их соответствующие медианы, а CAE
и LAB
— соответствующие углы, следовательно, \angle CAK=\angle CAE=\angle LAB
.
Обозначим
\angle MAB=\angle LAB=\angle CAK=\varphi,~\angle LAC=\angle NAC=\alpha.
Тогда
\angle LAK=\alpha-\varphi,~\angle MAK=2\varphi+(\alpha-\varphi)=\alpha+\varphi=\angle NAK.
Значит, AK
— биссектриса угла MAN
, а так как треугольники KAN
и KAM
равны по двум сторонам и углу между ними, то KM=KN
.
С другой стороны, из симметрии \angle MTB=\angle LTB=\angle ATK
, поэтому точка T
лежит на отрезке KM
. Тогда KM=KT+TL
, т. е. периметр треугольника KTL
равен
KM+KL=KN+KL=NL=NC+CL=CL+LB=BC=1.
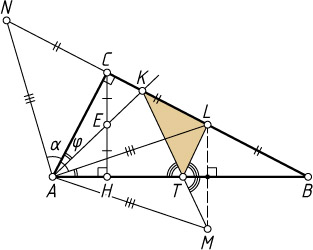
Автор: Кухарчук И. А.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2021, XVII, задача 1, 8 класс
