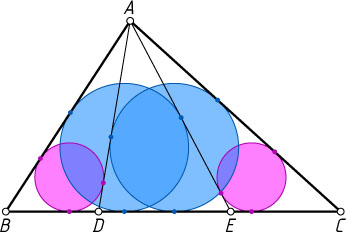
12123. а) В треугольнике ABC
на стороне BC
взяты точки D
и E
. Докажите, что если окружности, вписанные в треугольники ABD
и ACE
, равны, то и окружности, вписанные в треугольники ABE
и ACD
, также равны (рис. 1).
б) В треугольнике ABC
на стороне BC
взяты точки D
и E
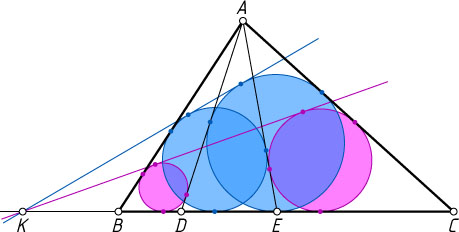
. Пусть K
— точка пересечения общих внешних касательных к окружностям, вписанным в треугольники ABD
и ACE
. Докажите, что K
также является точкой пересечения общих внешних касательных к окружностям, вписанным в треугольники ABE
и ACD
(рис. 2).
Решение. В некотором смысле пункт б) обобщает пункт а), поэтому сначала приведём решение пункта б).
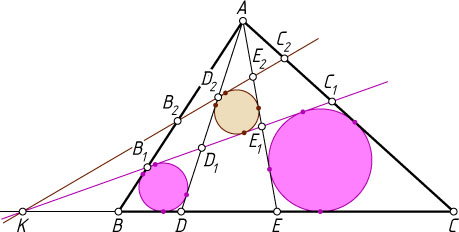
б) Пусть точки на прямой BC
следуют в порядке K
, B
, D
, E
, C
(рис. 3). Пусть касательная к вписанным окружностям треугольников ABD
и ACE
, проведённая из точки K
(и отличная от прямой BC
), пересекает AB
, AD
, AE
, AC
в точках B_{1}
, D_{1}
, E_{1}
, C_{1}
соответственно. Пусть \omega
— окружность, вписанная в треугольник AD_{1}E
. Проведём из точки K
касательную к окружности \omega
(отличную от прямой B_{1}C_{1}
). Пусть она пересекает отрезки AB
, AD
, AE
, AC
в точках B_{2}
, D_{2}
, E_{2}
, C_{2}
соответственно. Тогда, согласно задаче 11244, четырёхугольники BEE_{2}B_{2}
и CDD_{2}C_{2}
описанные, откуда и вытекает утверждение задачи.
а) Предположим, что окружности, вписанные в треугольники ABE
и ACD
, не равны. Тогда прямая BC
и вторая их общая внешняя касательная пересекаются в некоторой точке. Но тогда прямая BC
и вторая общая внешняя касательная вписанных окружностей треугольников ABD
и ACE
также пересекаются в этой точке, что невозможно.
Примечание. 1. Это решение было опубликовано в 1989 году в журнале Mathematics Magazine (см. статью: H.Demir, C.Tezer «More on incircles»).
2. См. также статью Н.Белухова и П.Кожевникова «Описанные четырёхугольники и ломаные», Квант, 2010, N1, с.45-49.
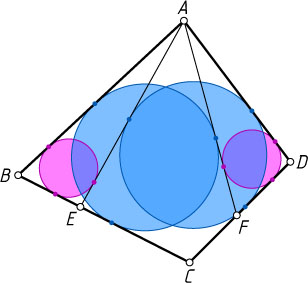
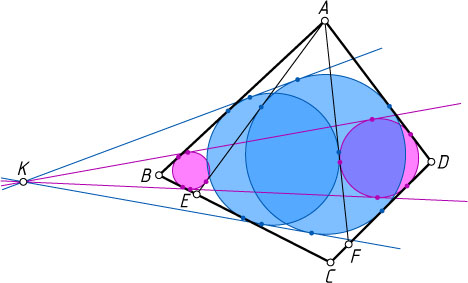
3. Н.Белухов обобщил эту задачу для описанного четырёхугольника таким образом. В описанном четырёхугольнике ABCD
на сторонах BC
и CD
взяты точки E
и F
. Пусть \omega_{b}
и \omega_{d}
— окружности, вписанные в треугольники ABE
и ADF
, \gamma_{b}
— окружность, касающаяся отрезков AB
, BC
, AF
, а \gamma_{d}
— окружность, касающаяся отрезков AD
, DC
, AE
(рис. 4).
а) Докажите, что окружности \omega_{b}
и \omega_{d}
равны тогда и только тогда, когда окружности \gamma_{b}
и \gamma_{d}
равны.
б) Пусть K
— точка пересечения общих внешних касательных к окружностям \omega_{b}
и \omega_{d}
. Докажите, что K
также является точкой пересечения общих внешних касательных к окружностям \gamma_{b}
и \gamma_{d}
(рис. 5).
Источник: Журнал «Квант». — 2012, № 1, с. 12




