1214. В треугольнике ABC
биссектриса угла A
пересекает сторону BC
в точке D
; прямая, проведённая через точку D
параллельно CA
, пересекает сторону AB
в точке E
; прямая, проведённая через точку E
параллельно BC
, пересекает сторону AC
в F
. Докажите, что EA=FC
.
Указание. Докажите, что треугольник AED
— равнобедренный.
Решение. Поскольку ED\parallel AC
, то \angle EDA=\angle CAD
, поэтому треугольник AED
— равнобедренный, EA=ED
.
Поскольку противоположные стороны четырёхугольника CDEF
попарно параллельны, то CDEF
— параллелограмм. Следовательно, FC=ED=EA
.
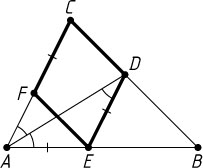
Источник: Погорелов А. В. Геометрия: Учебное пособие для 7—11 кл. средней школы. — 8-е изд. — М.: Просвещение, 1989. — № 89, с. 27
