12140. Дан прямоугольный треугольник ABC
с прямым углом при вершине C
. Окружность с диаметром AC
пересекает гипотенузу в точках A
и D
.
а) Докажите, что касательная, проведённая к окружности в точке D
, проходит через середину катета BC
.
б) Пусть эта касательная пересекает прямую AC
в точке P
, O
— центр окружности, а K
— точка пересечения прямых OM
и BP
. Найдите отношение BK:KP
, если \cos\angle BAC=\frac{4}{5}
.
Ответ. 7:25
.
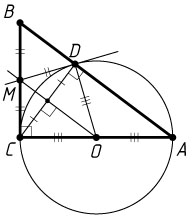
Решение. а) Пусть O
— центр окружности, а касательная к окружности, проведённая через точку D
, пересекает катет BC
в точке M
. Тогда MC=MD
как отрезки касательных, проведённых к окружности из одной точки, а так как OC=OD
как радиусы окружности, то прямая OM
— серединный перпендикуляр к отрезку CD
. При этом AB\perp CD
, а O
— середина AC
, значит, по теореме Фалеса M
— середина BC
. Что и требовалось доказать.
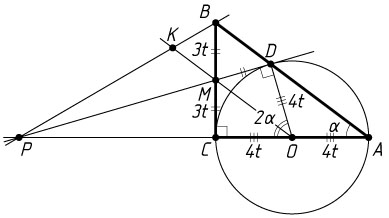
б) Положим \angle BAC=\alpha
, AC=8t
и AB=10t
. Тогда
BC=6t,~CM=3t,~OD=OC=4t,~\angle COD=2\angle CAB=2\alpha.
Из прямоугольного треугольника ODP
находим, что
OP=\frac{OD}{\cos\angle POD}=\frac{4t}{\cos2\alpha}=\frac{4t}{2\cos^{2}\alpha-1}=\frac{4t}{\frac{32}{25}-1}=\frac{100t}{7}.
Первый способ. По теореме о пропорциональных отрезках
\frac{BK}{KP}=\frac{AO}{OP}=\frac{4t}{\frac{100t}{7}}=\frac{7}{25}.
Второй способ. Искомое отношение можно найти, применив теорему Менелая к треугольнику BCP
и прямой OM
.
Источник: ЕГЭ. — 2021, 29 июня, задача 16

