12143. Дан параллелограмм ABCD
с острым углом A
. На продолжении стороны AD
за точку D
взята такая точка N
, что CN=CD
, а на продолжении стороны CD
за точку D
взята такая точка M
, что AD=AM
.
а) Докажите, что BM=BN
.
б) Найдите MN
, если AC=4
, \sin\angle BAD=\frac{8}{17}
.
Ответ. \frac{120}{17}
.
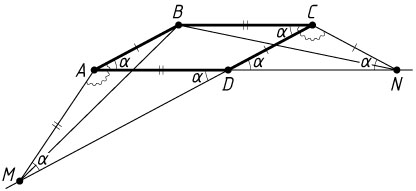
Решение. а) Обозначим \angle A=\alpha
. Треугольник DCN
равнобедренный (CN=CD
), поэтому
\angle CND=\angle CDN=\angle BCD=\alpha,~\angle DCN=180^{\circ}-2\alpha.
Значит,
\angle BCN=\alpha+(180^{\circ}-2\alpha)=180^{\circ}-\alpha.
Аналогично, \angle MAB=180^{\circ}-\alpha
, а так как
AB=CD=CN,~BC=AD=AM,
то треугольники BCN
и MAB
равны по двум сторонам и углу между ними. Следовательно, BM=BN
. Что и требовалось доказать.
б) По условию \sin\alpha=\frac{8}{17}
, поэтому \cos\alpha=\frac{15}{17}
. Поскольку ABCN
равнобокая трапеция, её диагонали равны, поэтому BM=BN=AC=4
. Из равенства треугольников BCN
и MAB
также следует, что \angle ABM=\angle CNB
, поэтому
\angle MBN=\angle ABC-\angle CBN-\angle ABM=
=\angle ABC-\angle CBN-\angle CNB=\angle ABC-(\angle CBN+\angle CNB)=
=\angle ABC-(180^{\circ}-\angle BCN)=(180^{\circ}-\alpha)-\alpha=180^{\circ}-2\alpha.
Значит,
\angle BMN=\frac{1}{2}(180^{\circ}-\angle MBN)=\alpha.
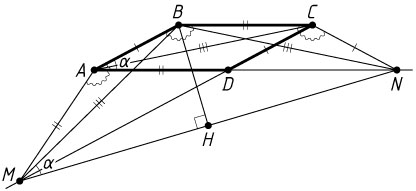
Пусть BH
— высота равнобедренного треугольника MBN
. Тогда
MN=2MH=2\cdot BM\cos\angle BMN=2\cdot4\cdot\cos\alpha=8\cdot\frac{15}{17}=\frac{120}{17}.
Источник: ЕГЭ. — 2021, задача 16

