12145. Высоты BB_{1}
и CC_{1}
остроугольного треугольника ABC
пересекаются в точке H
. Отрезок AP
— диаметр окружности, описанной около треугольника ABC
.
а) Докажите, что точки H
, P
и середина стороны BC
лежат на одной прямой.
б) Луч PH
пересекает окружность, описанную около треугольника ABC
, в точке M
. Найдите MC_{1}
, если расстояние от центра O
этой окружности до прямой BC
равно 4, \angle BPH=30^{\circ}
.
Ответ. 4
.
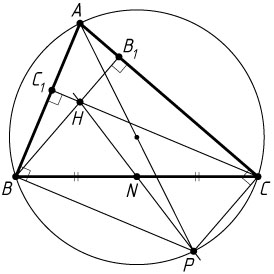
Решение. а) Точка C
лежит на окружности с диаметром AP
, поэтому \angle ACP=90^{\circ}
. Прямые BH
и PC
перпендикулярны прямой AC
, значит, BH\parallel PC
. Аналогично, CH\parallel PB
. Тогда BPCH
— параллелограмм. Его диагональ PH
проходит через середину N
диагонали BC
. Следовательно, точки H
, P
и N
лежат на одной прямой.
б) Отрезок ON
перпендикулярен стороне BC
, поэтому расстояние от точки O
до прямой BC
равно его длине, т. е. ON=4
. Поскольку O
и N
— середины сторон соответственно PA
и PH
треугольника APH
, отрезок OP
— средняя линия этого треугольника. Значит, AH=2ON=8
.
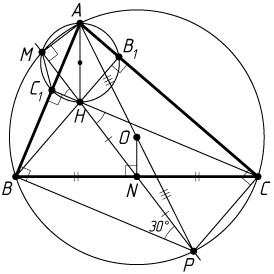
Точка M
лежит на окружности с диаметром AP
, поэтому \angle AMH=\angle AMP=90^{\circ}
. Из точек B_{1}
, C_{1}
и M
отрезок AH
виден под прямым углом, значит, эти точки лежат на окружности с диаметром AH
. Поскольку
\angle MHC_{1}=\angle PHC=\angle BPH=30^{\circ},
то по теореме синусов
MC_{1}=AH\sin\angle MHC_{1}=8\sin30^{\circ}=8\cdot\frac{1}{2}=4.
Источник: ЕГЭ. — 2021, досрочный экзамен, задача 16

