12168. В окружности проведены две непересекающиеся хорды равные радиусу.
а) Докажите, что концы данных хорд образуют трапецию или прямоугольник.
б) Найдите отношение большего основания этой трапеции к меньшему, если угол между прямыми, содержащими хорды, равен 30^{\circ}
.
Ответ. (1+\sqrt{3}):2
.
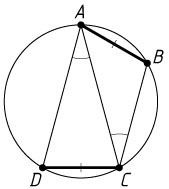
Решение. а) Пусть AB
и CD
— непересекающиеся хорды, равные радиусу окружности с центром O
, причём точки A
, B
, C
и D
расположены на окружности именно в этом порядке. Проведём диагональ AC
четырёхугольника ABCD
. Вписанные углы ACB
и DAC
опираются на равные хорды, поэтому они равны. Следовательно, BC\parallel AD
. Следовательно, ABCD
— трапеция или прямоугольник.
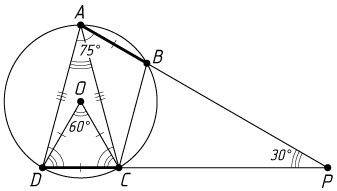
б) Пусть лучи AB
и DC
пересекаются в точке P
. Тогда ABCD
— трапеция с основаниями AD
и BC
(AD\gt BC
), вписанная в окружность. Она равнобедренная, поэтому
\angle PAD=\angle BAD=\angle CDA=\angle PDA=\frac{180^{\circ}-30^{\circ}}{2}=75^{\circ}.
Треугольник COD
равносторонний, поэтому \angle COD=60^{\circ}
, а так как вписанный угол равен половине соответствующего центрального, то
\angle CAD=30^{\circ},~\angle ACD=180^{\circ}-75^{\circ}-30^{\circ}=75^{\circ}=\angle ADC.
Значит, AC=AD
.
Учитывая, что AC=AD
, по теореме синусов для треугольника ABC
получим
\frac{AD}{BC}=\frac{AC}{BC}=\frac{\sin\angle ABC}{\sin\angle BAC}=\frac{\sin(180^{\circ}-75^{\circ})}{\sin(75^{\circ}-30^{\circ})}=\frac{\sin75^{\circ}}{\sin45^{\circ}}=\frac{\sin(45^{\circ}+30^{\circ})}{\sin45^{\circ}}=
=\frac{\sin45^{\circ}\cos30^{\circ}+\cos45^{\circ}\sin30^{\circ}}{\sin45^{\circ}}=\cos30^{\circ}+\ctg45^{\circ}\sin30^{\circ}=\frac{\sqrt{3}+1}{2}.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2021, 11 класс, задача 16

