12178. Вокруг равнобедренного остроугольного треугольника NPQ
с основанием NQ
описана окружность \Omega
. Точка F
— середина дуги PN
, не содержащей точки Q
. Известно, что расстояния от точки F
до прямых PN
и QN
, равны соответственно 5 и \frac{20}{3}
. Найдите радиус окружности \Omega
и площадь треугольника NPQ
.
Ответ. R=6
, S=\frac{35\sqrt{35}}{9}
.
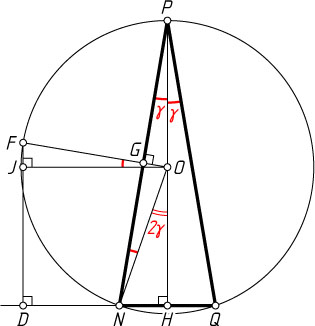
Решение. Пусть O
— центр окружности, R
— её радиус, G
— точка пересечения отрезков OF
и NP
(тогда G
— середина NP
и при этом OG\perp NP
); PH
— высота треугольника (точка O
лежит на отрезке PH
, так как треугольник NPQ
остроугольный), FD
— перпендикуляр, опущенный из точки F
на прямую NQ
, OJ
— перпендикуляр, опущенный из точки O
на прямую FD
. Обозначим \angle NPH=\gamma
. Тогда
OG=OP\sin\gamma=R\sin\gamma,~FG=OF-OG=R-R\sin\gamma=R(1-\sin\gamma),
FJ=OF\sin\gamma=R\sin\gamma.
Треугольник OPN
равнобедренный (ON=OP=R
), поэтому \angle ONP=\angle OPN
, и по теореме о внешнем угле треугольника \angle NOH=2\gamma
. Значит,
OH=ON\cos2\gamma=R\cos2\gamma,~DJ=OH=R\cos2\gamma
(JDHO
— прямоугольник). Тогда
FD=FJ+JD=R(\sin\gamma+\cos2\gamma)=R(1+\sin\gamma-2\sin^{2}\gamma)=
=R(1-\sin\gamma)(1+2\sin\gamma).
По условию
R(1-\sin\gamma)=5,~R(1-\sin\gamma)(1+2\sin\gamma)=\frac{20}{3}.
Разделив второе уравнение на первое, получаем
1+2\sin\gamma=\frac{4}{3},~\sin\gamma=\frac{1}{6},~\cos\gamma=\frac{\sqrt{35}}{6}.
Следовательно,
R=\frac{5}{1-\sin\gamma}=\frac{5}{1-\frac{1}{6}}=6,
S_{\triangle NPQ}=NH\cdot PH=ON\sin2\gamma\cdot(OP+OH)=R\sin2\gamma\cdot(R+R\cos2\gamma)=
=4R^{2}\sin\gamma\cos\gamma\cdot\cos^{2}\gamma=4R^{2}\sin\gamma\cos^{3}\gamma=4\cdot6^{2}\cdot\frac{35\sqrt{35}}{6^{3}}\cdot\frac{1}{6}=\frac{35\sqrt{35}}{9}.
Источник: Олимпиада «Физтех» (математическая олимпиада МФТИ). — 2016, 10 класс, билет 5, задача 6
