1219. Перпендикуляр, опущенный из вершины прямоугольника на его диагональ, делит её в отношении 1:3
. Найдите диагональ, если известно, что точка её пересечения с другой диагональю удалена от большей стороны на расстояние, равное 2.
Ответ. 8.
Указание. Меньшая сторона прямоугольника равна 4.
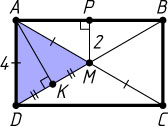
Решение. Пусть M
— точка пересечения диагоналей AC
и BD
прямоугольника ABCD
, AB
— большая его сторона, AK
— перпендикуляр, опущенный из точки A
на диагональ DB
, P
— середина AB
. Тогда
AD=2MP=4,~DK=\frac{1}{4}DB=\frac{1}{2}DM,
т. е. K
— середина DM
. Поэтому высота AK
треугольника DAM
является его медианой. Следовательно, треугольник DAM
— равнобедренный, AM=AD=4
. Тогда AC=2AM=8
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 29, с. 21
