1224. Найдите диагонали четырёхугольника, образованного биссектрисами внутренних углов прямоугольника со сторонами 1 и 3.
Ответ. 2.
Указание. Полученный четырёхугольник — квадрат.
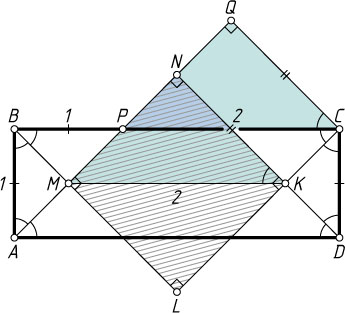
Решение. Пусть ABCD
— данный прямоугольник, AB=1
, BC=3
.
Четырёхугольник MNKL
, образованный пересечением биссектрис углов A
и B
, A
и D
, C
и D
, B
и C
, — квадрат.
Пусть P
— точка пересечения биссектрисы угла A
со стороной BC
, Q
— основание перпендикуляра, опущенного из вершины C
на прямую AP
. Поскольку
BP=AB=1,~PC=BC-BP=2,
то из равенства треугольников PQC
и MNK
(по катету и острому углу) следует, что MK=PC=2
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 50(2), с. 23
