1226. Основания трапеции равны a
и b
(a\gt b
). Найдите длину отрезка, соединяющего середины диагоналей трапеции.
Ответ. \frac{a-b}{2}
.
Указание. Соедините середины диагоналей с серединой одной из боковых сторон трапеции.
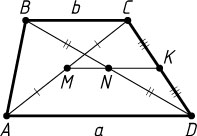
Решение. Пусть M
и N
— середины диагоналей AC
и BD
трапеции ABCD
, в которой AD=a
и BC=b
.
Соединим точку M
с серединой K
боковой стороны CD
. По теореме о средней линии треугольника MK\parallel AD\parallel BC
. Аналогично докажем, что NK\parallel BC
.
Поскольку через точку, не лежащую на прямой, можно провести не более одной прямой, параллельной данной, то точки M
, N
и K
лежат на одной прямой. Эта прямая параллельна основаниям трапеции.
Таким образом,
MN=MK-KN=\frac{1}{2}AD-\frac{1}{2}BC=\frac{a-b}{2}.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 34 (фрагмент), с. 64
Источник: Шарыгин И. Ф. Геометрия 7—9: Учебник для общеобразовательных учебных заведений. — М.: Дрофа, 2002. — № 16, с. 158
Источник: Задачи по математике и физике, дававшиеся на приёмных испытаниях в 1947—1953 гг. — М.: МФТИ, 1956. — 1953, билет 4, № 3, с. 8
Источник: Погорелов А. В. Геометрия: Учебное пособие для 7—11 кл. средней школы. — 8-е изд. — М.: Просвещение, 1989. — № 60, с. 80
Источник: Вступительный экзамен в МИЭТ. — 1977
Источник: Говоров В. М. и др. Сборник конкурсных задач по математике. — М.: Наука, 1986. — № 23, с. 186
Источник: Вступительный экзамен в МФТИ. — 1953, № 3, билет 14
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.10, с. 30
