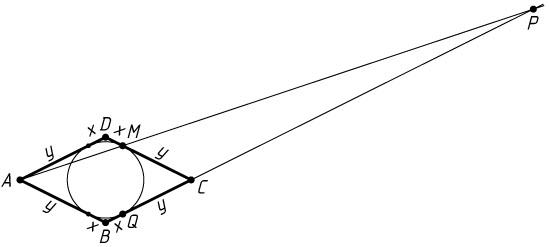
12300. Окружность, вписанная в ромб ABCD
, касается сторон CD
и BC
в точках M
и Q
соответственно. Прямые AM
и BC
пересекаются в точке P
.
а) Докажите, что BP\cdot BQ=BC^{2}
.
б) Найдите угол APC
, если DM:MC=1:4
.
Ответ. \arcctg7
.
Решение. а) Обозначим DM=BQ=x
, CM=y
. Треугольники CMP
и DMA
подобны с коэффициентом \frac{CM}{MD}=\frac{y}{x}
, поэтому
CP=\frac{y}{x}\cdot AD=\frac{y(x+y)}{x}.
Тогда
BP=BC+CP=x+y+\frac{y(x+y)}{x}=(x+y)\left(1+\frac{y}{x}\right)=\frac{(x+y)^{2}}{x}=\frac{BC^{2}}{BQ}.
Следовательно, BP\cdot BQ=BC^{2}
.
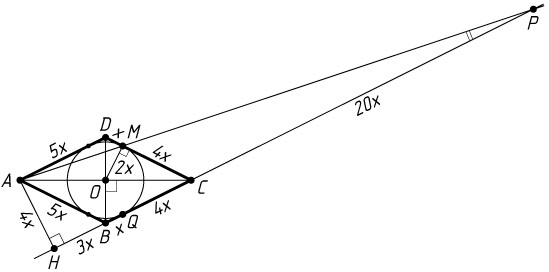
б) Положим DM=x
, MC=4x
. Пусть O
— центр окружности, радиуса r
, вписанной в ромб. Тогда OM
— высота прямоугольного треугольника COD
, проведённая из вершины угла, поэтому
r=OM=\sqrt{DM\cdot MC}=\sqrt{x\cdot4x}=2x.
Значит, высота ромба равна 2r=4x
.
Пусть H
— основание перпендикуляра, опущенного из вершины A
на прямую BC
. Тогда AH
— высота ромба, поэтому
AH=2r=4x,~BH=\sqrt{AB^{2}-AH^{2}}=\sqrt{25x^{2}-16x^{2}}=3x.
Из подобия треугольников CMP
и DMA
находим, что
CP=\frac{CM}{MD}\cdot AD=4\cdot5x=20x.
Значит,
PH=CP+BC+BH=20x+5x+3x=28x.
Из прямоугольного треугольника AHP
находим, что
\ctg\angle APH=\frac{PH}{AH}=\frac{28x}{4x}=7.
Следовательно,
\angle APC=\angle APH=\arcctg7.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2019

