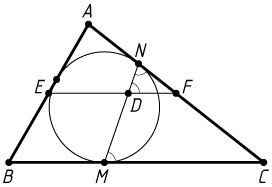
12320. Окружность, вписанная в треугольник ABC
, касается сторон AB
и AC
в точках M
и N
соответственно, E
и F
— середины сторон AB
и AC
соответственно. Прямые MN
и EF
пересекаются в точке D
.
а) Докажите, что треугольник DFN
равнобедренный.
б) Найдите площадь треугольника BED
, если AB=20
и \angle ABC=60^{\circ}
.
Ответ. 25\sqrt{3}
.
Решение. а) Поскольку CM=CN
, треугольник MCN
равнобедренный. Прямые EF
и BC
параллельны, поэтому треугольник DFN
подобен треугольнику MCN
, следовательно, треугольник DFN
также равнобедренный, DF=NF
.
б) Обозначим BC=a
, AC=b
, AB=c
. Пусть p
— полупериметр треугольника ABC
. Предположим, что a\gt c
. Тогда
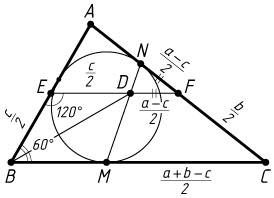
BE=\frac{c}{2},~CF=\frac{b}{2},~CM=CN=p-c=\frac{a+b-c}{2},
FD=FN=CN-CF=\frac{a+b-c}{2}-\frac{b}{2}=\frac{a-c}{2}.
Значит,
ED=EF-FD=\frac{a}{2}-\frac{a-c}{2}=\frac{c}{2}=BE,
т. е. треугольник BED
равнобедренный.
Аналогично для a\leqslant c
.
Поскольку прямые ED
и BC
параллельны,
\angle BED=180^{\circ}-\angle ABC=180^{\circ}-60^{\circ}=120^{\circ}.
Следовательно,
S_{\triangle BED}=\frac{1}{2}BE\cdot ED\sin120^{\circ}=\frac{1}{2}\cdot10\cdot10\cdot\frac{\sqrt{3}}{2}=25\sqrt{3}.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2019

