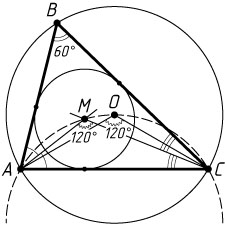
12324. В остроугольном треугольнике ABC
угол B
равен 60^{\circ}
. Точка O
— центр описанной окружности треугольника ABC
, точка M
— центр вписанной окружности.
а) Докажите, что точки A
, O
, M
, C
лежат на одной окружности.
б) Найдите отношение BM:BO
, если \cos\angle ACB=\frac{3}{5}
.
Ответ. \frac{4\sqrt{3}-2}{5}
.
Решение. а) Заметим, что AOC
— центральный угол описанной окружности данного треугольника, соответствующий вписанному углу ABC
, поэтому
\angle AOC=2\angle ABC=120^{\circ}.
В то же время,
\angle AMC=90^{\circ}+\frac{1}{2}\angle ABC=90^{\circ}+30^{\circ}=120^{\circ},
так как лучи AM
и CM
— биссектрисы углов треугольника ABC
. Таким образом, из точек O
и M
, лежащих по одну сторону от прямой AC
, отрезок AC
виден под одним и тем же углом. Следовательно, точки A
, O
, M
, C
лежат на одной окружности.
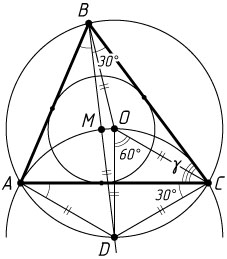
б) Пусть луч BM
— биссектриса вписанного угла ABC
— пересекает описанную окружность в точке D
. Отрезки AD
и DC
равны как хорды, стягивающие равные дуги, а так как DOC
— центральный угол, соответствующий вписанному углу DBC
, то
\angle DOC=2\angle DBC=60^{\circ}.
Значит, треугольник DOC
равносторонний, и OD=DC
.
Точка D
равноудалена от точек C
, O
и A
, т. е. D
— центр окружности, на которой лежат эти точки, а также точка M
.
Пусть R
— радиус окружности, описанной около треугольника ABC
, а \angle ACB=\gamma
. Тогда
DC=DM=OD=R,~\cos\gamma=\frac{3}{5},~\sin\gamma=\frac{4}{5}.
Из треугольника BDC
по теореме синусов получаем
2R=\frac{BD}{\sin\angle BCD}=\frac{BM+MD}{\sin(\angle ACB+\angle ACD)}=
=\frac{BM+R}{\sin(\angle ACB+\angle ABD)}=\frac{BM+R}{\sin(\gamma+30^{\circ})}.
Значит,
BM+R=2R\sin(\gamma+30^{\circ})=2R(\sin\gamma\cos30^{\circ}+\cos\gamma\sin30^{\circ})=
=2R\left(\frac{4}{5}\cdot\frac{\sqrt{3}}{2}+\frac{3}{5}\cdot\frac{1}{2}\right)=2R\left(\frac{2\sqrt{3}}{5}+\frac{3}{10}\right),
откуда
BM=2R\left(\frac{2\sqrt{3}}{5}+\frac{3}{10}\right)-R=\frac{R(4\sqrt{3}-2)}{5}.
Следовательно,
\frac{BM}{BO}=\frac{\frac{R(4\sqrt{3}-2)}{5}}{R}=\frac{4\sqrt{3}-2}{5}.
