12325. В параллелограмме ABCD
расположены две равные непересекающиеся окружности. Первая касается сторон AD
, AB
и BC
, а вторая — сторон AD
, CD
и BC
.
а) Докажите, что общая внутренняя касательная l
окружностей проходит через центр параллелограмма.
б) Пусть ABCD
— прямоугольник, а прямая l
касается окружностей в точках M
и N
. Найдите площадь четырёхугольника с вершинами в точках M
, N
и в центрах окружностей, если AD=16
, а расстояние между центрами окружностей равно 10
.
Ответ. 24
.
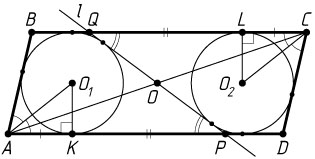
Решение. а) Пусть O
— точка пересечения диагонали AC
параллелограмма с общей внутренней касательной l
к данным окружностям (рис. 1), P
и Q
точки пересечения прямой l
со сторонами AD
и BC
соответственно. Достаточно доказать что O
— середина диагонали AC
.
Пусть O_{1}
и O_{2}
— центры первой и второй окружностей, первая окружность касается стороны AD
в точке K
, вторая окружность касается стороны BC
в точке L
. Лучи AO_{1}
и CO_{2}
— биссектрисы равных углов BAD
и BCD
, значит, прямоугольные треугольники AKO_{1}
и CLO_{2}
равны по катету (радиусы равных окружностей) и противолежащему острому углу. Тогда AK=CL
. Аналогично, KP=LQ
. Следовательно,
AP=AK+KP=CL+LQ=CQ.
Значит, треугольники AOP
и COQ
равны по стороне и двум прилежащим к ней углам, поэтому AO=OC
, а O
— середина диагонали AC
, т. е. центр параллелограмма ABCD
.
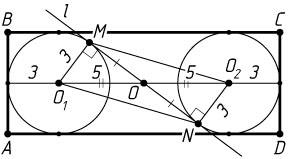
б) Поскольку ABCD
прямоугольник (рис. 2), его сторона AD
равна сумме диаметра окружности и отрезка O_{1}O_{2}
, т. е. 2r+O_{1}O_{2}=AD
, или 2r+10=16
, откуда r=3
.
Четырёхугольник O_{1}MO_{2}N
— параллелограмм, так как его противоположные стороны O_{1}M
и O_{2}N
равны и параллельны. Диагонали O_{1}O_{2}
и MN
параллелограмма O_{1}MO_{2}N
пересекаются в точке O
и делятся ею пополам Площадь параллелограмма O_{1}MO_{2}N
в четыре раза больше площади прямоугольного треугольника OO_{1}M
, в котором
OO_{1}=\frac{1}{2}O_{1}O_{2}=5,~O_{1}M=r=3.
По теореме Пифагора
OM=\sqrt{OO_{1}^{2}-O_{1}M^{2}}=\sqrt{5^{2}-3^{2}}=4.
Следовательно,
S_{O_{1}MO_{2}N}=4S_{\triangle OO_{1}M}=4\cdot\frac{1}{2}OM\cdot O_{1}M=2\cdot4\cdot3=24.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2021

