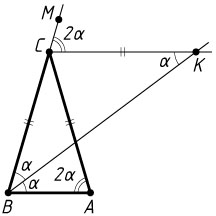
12327. Биссектриса внешнего угла при вершине C
остроугольного треугольника ABC
пересекает биссектрису внутреннего угла при вершине B
в точке K
. Известно, что BC=CK
.
а) Докажите, что треугольник ABC
равнобедренный.
б) Найдите площадь четырёхугольника ABCK
, если AB=7
, AK=15
.
Ответ. 117.
Решение. а) Обозначим
\angle BKC=\angle CBK=\angle ABK=\alpha.
Пусть M
— точка на продолжении стороны BC
за точку C
. По теореме о внешнем угле треугольника,
\angle ACK=\angle KCM=2\angle CBK=2\alpha=\angle ABC.
Значит, прямые AB
и CK
параллельны, поэтому
\angle BAC=\angle ACK=2\alpha=\angle ABC.
Следовательно, треугольник ABC
равнобедренный, BC=AC
.
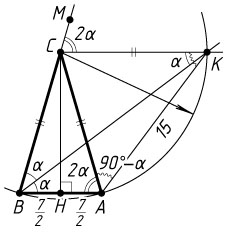
б) Четырёхугольник ABCK
— трапеция с основаниями AB=7
и CK
. Точка C
— центр окружности, описанной около треугольника ABK
, так как CB=CA=CK
. Тогда из равнобедренного треугольника ACK
получаем, что
\angle KAC=\angle AKC=90^{\circ}-\alpha,
а так как вписанный угол AKB
равен половине соответствующего центрального угла ACB
, то
\angle AKB=\frac{1}{2}\angle ACB=\frac{1}{2}(180^{\circ}-4\alpha)=90^{\circ}-2\alpha.
По теореме синусов из треугольника ABK
получаем, что
\frac{AK}{\sin\alpha}=\frac{AB}{\sin(90^{\circ}-2\alpha)},~\frac{15}{\sin\alpha}=\frac{7}{\cos2\alpha},~\frac{15}{\sin\alpha}=\frac{7}{1-2\sin^{2}\alpha},
30\sin^{2}\alpha+7\sin\alpha-15=0,
откуда \sin\alpha=\frac{3}{5}
. Тогда
AC=BC=CK=\frac{\frac{1}{2}AK}{\sin\frac{1}{2}\angle ACK}=\frac{15}{2\sin\alpha}=\frac{15}{2\cdot\frac{3}{5}}=\frac{25}{2}.
Проведём высоту CH
из вершины C
равнобедренного треугольника ABC
. Из прямоугольного треугольника BCH
находим, что
CH=\sqrt{BC^{2}-BH^{2}}=\sqrt{\frac{625}{4}-\frac{49}{4}}=12,
а так как CH
— высота трапеции ABCK
, то
S_{ABCK}=\frac{AB+CK}{2}\cdot CH=\frac{7+\frac{25}{2}}{2}\cdot12=117.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2021

