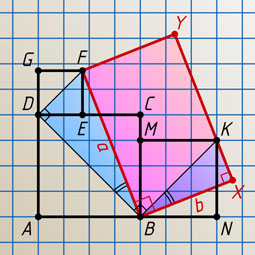
12330. Три квадрата — ABCD
со стороной 4, BNKM
со стороной 3 и DEFG
со стороной, меньшей 3, расположены так, как показано на рисунке. Найдите площадь прямоугольника BXYF
(точка M
лежит на отрезке BC
, E
— на CD
, D
— на AG
, B
— на AN
, K
— на XY
).
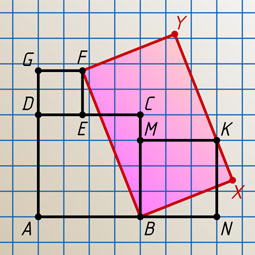
Ответ. 24.
Решение. Первый способ. Обозначим BF=a
и BX=b
(рис. 1). Диагональ квадрата образует с его стороной угол 45^{\circ}
, поэтому
\angle BDF=\angle DBK=90^{\circ}.
Тогда
\angle KBX=90^{\circ}-\angle FBK=\angle DBK-\angle FBK=\angle FBD,
значит, \cos\angle KBX=\cos\angle FBD
, т. е. \frac{BX}{BK}=\frac{BD}{BF}
, или \frac{b}{3\sqrt{2}}=\frac{4\sqrt{2}}{a}
. Следовательно,
S_{BXYF}=ab=3\sqrt{2}\cdot4\sqrt{2}=24.
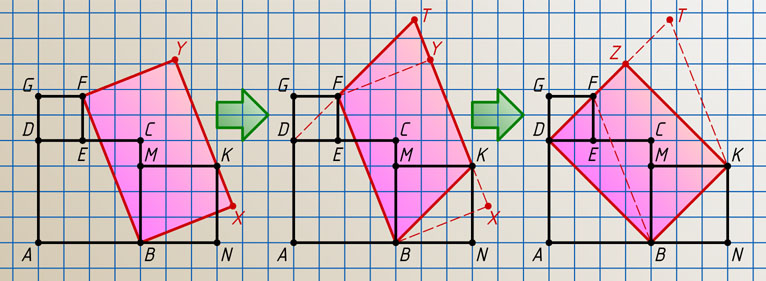
Второй способ. Прямоугольник BXYF
и параллелограмм FBKT
равновелики (рис. 2), так как BF
— их общая сторона, а BX
— общая высота. Параллелограмм FBKT
и прямоугольник DBKZ
равновелики, так как BK
— их общая сторона, а BD
— общая высота. Значит, прямоугольник BXYF
равновелик прямоугольнику DBKZ
, площадь которого равна
BK\cdot BD=3\sqrt{2}\cdot4\sqrt{2}=24.