12337. В окружности проведены диаметр PQ
и отличная от него хорда AT
, перпендикулярные хорде BC
(см. рис.). Докажите, что
\frac{AQ}{PQ}=\frac{AB+AC}{PB+PC}=\frac{TB+TC}{QB+QC}.
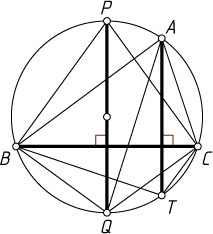
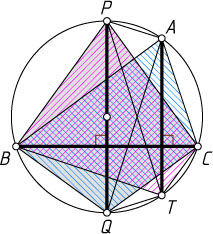
Решение. Заметим, что
PB=PC,~QB=QC,
а так как вписанная трапеция APQT
равнобедренная, то AQ=PT
. Тогда по теореме Птолемея из вписанных четырёхугольников ABQC
, BTCP
и BQCP
получаем
BC\cdot AQ=AB\cdot QC+AC\cdot QB=AB\cdot QB+AC\cdot QB=QB(AB+AC),
BC\cdot AQ=BC\cdot PT=PC\cdot TB+PB\cdot TC=PB(TB+TC),
BC\cdot PQ=PB\cdot QC+PC\cdot QB=QB(PB+PC),
BC\cdot PQ=PB\cdot QC+PC\cdot QB=PB(QB+QC).
Разделив первое из этих равенств на третье, получим
\frac{AQ}{PQ}=\frac{AB+AC}{PB+PC},
а разделив второе на четвёртое, получим
\frac{AQ}{PQ}=\frac{TB+TC}{QB+QC}.
Отсюда следует утверждение задачи.
Источник: Журнал «Crux Mathematicorum». — 1981, № 8, задача 580, с. 253

