1236. Основание AB
трапеции ABCD
вдвое больше основания CD
и вдвое больше боковой стороны AD
. Диагональ AC
равна a
, а боковая сторона BC
равна b
. Найдите площадь трапеции.
Ответ. \frac{3}{4}ab
.
Указание. Проведите через точку D
прямую, параллельную BC
.
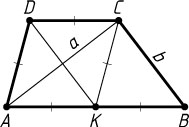
Решение. Через вершину D
проведём прямую, параллельную BC
. Пусть K
— точка пересечения проведённой прямой с основанием AB
. Тогда ADCK
— ромб, а DCBK
— параллелограмм. Поэтому
DK=BC=b,~S_{ADCK}=\frac{1}{2}DK\cdot AC=\frac{1}{2}ab,
S_{\triangle KCB}=S_{\triangle AKC}=\frac{1}{2}S_{ADCK}=\frac{1}{4}ab.
Следовательно, S_{ABCD}=\frac{3}{4}ab
.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1977, вариант 1, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 59
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.29, с. 32
