1237. В параллелограмме со сторонами a
и b
и углом \alpha
проведены биссектрисы четырёх углов. Найдите площадь четырёхугольника, ограниченного этими биссектрисами.
Ответ. \frac{1}{2}(a-b)^{2}\sin\alpha
.
Указание. Четырёхугольник, ограниченный указанными биссектрисами, — прямоугольник.
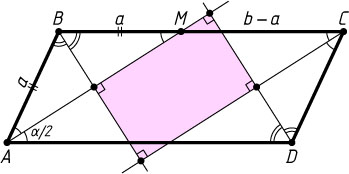
Решение. Первый способ. Пусть биссектриса угла A
параллелограмма ABCD
пересекает сторону BC
в точке M
(рис. 1), \angle BAD=\alpha
(\alpha\lt90^{\circ}
), AB=a
, BC=b
и b\gt a
. Тогда
\angle BMA=\angle MAD=\angle MAB=\frac{\alpha}{2}.
Следовательно, треугольник ABM
— равнобедренный и BM=AB=a
. Поэтому MC=b-a
.
Расстояние между проведённой биссектрисой и биссектрисой угла BCD
равно
MC\sin\frac{\alpha}{2}=(b-a)\sin\frac{\alpha}{2}.
Аналогично найдём, что расстояние между биссектрисами углов B
и D
равно (b-a)\cos\frac{\alpha}{2}
.
Четырёхугольник, ограниченный указанными биссектрисами, — прямоугольник со сторонами, равными
(b-a)\sin\frac{\alpha}{2},~(b-a)\cos\frac{\alpha}{2}.
Следовательно, его площадь равна
(b-a)\sin\frac{\alpha}{2}\cdot(b-a)\cos\frac{\alpha}{2}=\frac{1}{2}(a-b)^{2}\sin\alpha.
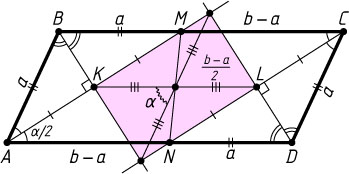
Второй способ. Пусть биссектриса угла A
параллелограмма ABCD
пересекает сторону BC
в точке M
(рис. 2), биссектриса угла C
пересекает сторону AD
в точке N
, \angle BAD=\alpha
(\alpha\lt90^{\circ}
), AB=a
, BC=b
и b\gt a
. Тогда
\angle BMA=\angle MAD=\angle MAB=\frac{\alpha}{2}.
Следовательно, треугольник ABM
— равнобедренный и BM=AB=a
. Поэтому MC=b-a
. Аналогично AN=b-a
.
Пусть K
— точка пересечения биссектрис углов A
и B
параллелограмма, а L
— точка пересечения биссектрис углов C
и D
. Тогда BK
— высота и медиана равнобедренного треугольника ABM
. Значит, BK\perp AM
и K
— середина AM
. Аналогично L
— середина CN
. Отрезок KL
, соединяющий середины противоположных сторон параллелограмма, AMCN
равен и параллелен отрезку MC
. Кроме того, этот отрезок — диагональ прямоугольника, образованного биссектрисами исходного параллелограмма. Вторая диагональ прямоугольника также равна b-a
и параллельна сторонам AB
и CD
, а угол между диагоналями прямоугольника равен углу между сторонами AB
и AD
параллелограмма, т. е. \alpha
. Площадь прямоугольника равна половине произведения его диагоналей на синус угла между ними, т. е. \frac{1}{2}(b-a)^{2}\sin\alpha
.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 29, с. 9
Источник: Вступительный экзамен в МИТХТ. — 1979

