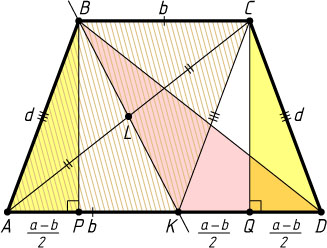
1241. В равнобедренной трапеции ABCD
основание AD
равно a
, основание BC
равно b
, AB=d
. Через вершину B
проведена прямая, делящая пополам диагональ AC
и пересекающая AD
в точке K
. Найдите площадь треугольника BDK
.
Ответ. \frac{1}{4}|a-b|\sqrt{4d^{2}-(a-b)^{2}}
.
Указание. Четырёхугольник ABCK
— параллелограмм.
Решение. Пусть a\gt b
. Поскольку ABCK
— параллелограмм, то
AK=BC=b,DK=AD-AK=a-b.
Опустим перпендикуляры BP
и CQ
из вершины B
и C
на AD
. Тогда BP
— высота трапеции и треугольника BDK
,
AP=DQ=\frac{1}{KD}=\frac{a-b}{2},
BP=\sqrt{AB^{2}-AP^{2}}=\sqrt{d^{2}-\frac{(a-b)^{2}}{4}}=\frac{1}{2}\sqrt{4d^{2}-(a-b)^{2}}.
Следовательно,
S_{\triangle BDK}=\frac{1}{2}KD\cdot BP=\frac{1}{4}(a-b)\sqrt{4d^{2}-(a-b)^{2}}.
Аналогично для случая a\lt b
.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 82, с. 13
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 82, с. 12
