12414. У крестообразно пересекающихся четырёхугольников соответствующие стороны параллельны и отстоят друг от друга на расстояние 1, как показано на рисунке. Докажите, что периметры четырёхугольников равны.
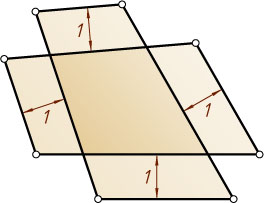
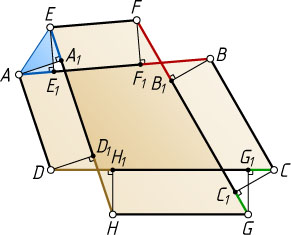
Решение. Пусть ABCD
и EFGH
— данные четырёхугольники, AA_{1}
, BB_{1}
, CC_{1}
, DD_{1}
, EE_{1}
, FF_{1}
, GG_{1}
, HH_{1}
— перпендикуляры к EH
, FG
, FG
, EH
, AB
, AB
, CD
, CD
соответственно (показано на рисунке). Прямоугольные треугольники AEE_{1}
и AEA_{1}
равны по гипотенузе и катету (AA_{1}=EE_{1}=1
), поэтому AE_{1}=A_{1}E
. Аналогично F_{1}B=FB_{1}
, CG_{1}=C_{1}G
, H_{1}D=HD_{1}
.
Из равенств
AB=AE_{1}+E_{1}F_{1}+F_{1}B=AE_{1}+EF+F_{1}B,~BC=FG-FB_{1}-C_{1}G,
CD=CG_{1}+G_{1}H_{1}+H_{1}D=CG_{1}+GH+H_{1}D,~DA=HE-HD_{1}-A_{1}E
следует, что
AB+BC+CD+DA=EF+FG+GH+HE+
+(AE_{1}-A_{1}E)+(F_{1}B-FB_{1})+(CG_{1}-C_{1}G)+(H_{1}D-HD_{1})=
=EF+FG+GH+HE.
Что и требовалось доказать.
Автор: Произволов В. В.
Источник: Летний турнир им. А. П. Савина «Математика 6—8». — 2001, задача 6, второй тур, 6-8 класс

