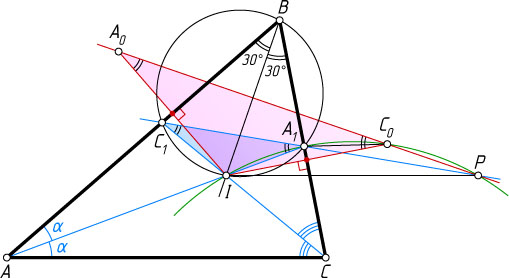
12424. В треугольнике ABC
угол B
равен 60^{\circ}
, биссектрисы AA_{1}
и CC_{1}
треугольника пересекаются в точке I
. Точки A_{0}
и C_{0}
симметричны точке I
относительно прямых AB
и CB
соответственно. Докажите, что если P
— точка пересечения прямых A_{1}C_{1}
и A_{0}C_{0}
, то прямые PI
и AC
параллельны.
Решение. В треугольнике A_{0}IC_{0}
стороны A_{0}I
и C_{0}I
равны удвоенному радиусу вписанной окружности треугольника ABC
, а
\angle A_{0}IC_{0}=180^{\circ}-\angle ABC=120^{\circ}.
Следовательно, треугольник A_{0}IC_{0}
равнобедренный с углом 30^{\circ}
при основании.
Четырёхугольник A_{1}BC_{1}I
вписанный, поскольку
\angle A_{1}IC_{1}=90^{\circ}+\frac{1}{2}\angle ABC
(см. задачу 4770), а так как \angle A_{1}BI=\angle C_{1}BI
, то хорды A_{1}I
и C_{1}I
стягивают равные дуги, поэтому они равны. Значит, и треугольник A_{1}IC_{1}
равнобедренный с углом 30^{\circ}
при основании.
Будем считать, что \angle BAC\lt\angle BCA
. Тогда указанные в условии точки расположены так, как показано на рисунке. Обозначим \angle A_{1}AB=\angle A_{1}AC=\alpha
. Тогда по теореме о внешнем угле треугольника
\angle AA_{1}C=\angle ABA_{1}+\angle A_{1}AB=60^{\circ}+\alpha,
\angle A_{1}C_{0}I=\angle A_{1}IC_{0}=90^{\circ}-(60^{\circ}+\alpha)=30^{\circ}-\alpha.
Поскольку
\angle IC_{0}P=180^{\circ}-\angle IC_{0}A_{0}=180^{\circ}-30^{\circ}=150^{\circ}
и
\angle IA_{1}P=180^{\circ}-\angle IA_{1}C_{1}=180^{\circ}-30^{\circ}=150^{\circ},
то четырёхугольник IA_{1}C_{0}P
вписанный (из точек C_{0}
и A_{1}
отрезок IP
виден под одним и тем же углом). Значит,
\angle A_{1}IP=180^{\circ}-\angle A_{1}C_{0}P=\angle A_{1}C_{0}A_{0}=\angle IC_{0}A_{0}-\angle A_{1}C_{0}I=
=30^{\circ}-(30^{\circ}-\alpha)=\alpha.
Получаем, что соответственные углы A_{1}IP
и A_{1}AC
равны, поэтому прямые PI
и AC
параллельны. Что и требовалось доказать.
Автор: Швецов Д. В.
Источник: Летний турнир им. А. П. Савина «Математика 6—8». — 2021, XXVI, 8 класс
Источник: Журнал «Квант». — 2021, № 9, с. 47, задача 16
