1243. Найдите площадь треугольника, если две его стороны равны 1 и \sqrt{15}
, а медиана, проведённая к третьей, равна 2.
Ответ. \frac{\sqrt{15}}{2}
.
Указание. На продолжении данной медианы AA_{1}
за точку A_{1}
отложите отрезок, равный AA_{1}
.
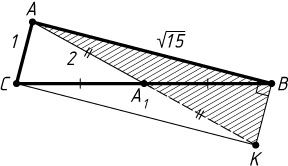
Решение. Пусть AA_{1}
— медиана треугольника ABC
, AA_{1}=2
, AB=\sqrt{15}
, AC=1
. На продолжении медианы AA_{1}
за точку A_{1}
отложим отрезок A_{1}K
, равный AA_{1}
. Тогда CABK
— параллелограмм, BK=AC=1
.
Треугольник ABK
— прямоугольный, так как AK^{2}=AB^{2}+BK^{2}
. Следовательно,
S_{\triangle ABC}=S_{\triangle ABK}=\frac{\sqrt{15}}{2}.
Источник: Вступительный экзамен на технологический факультет МИСиС. — 1980
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 13
