1244. В трапеции ABCD
диагонали AC
и BD
взаимно перпендикулярны, \angle BAC=\angle CDB
. Продолжения боковых сторон AB
и DC
пересекаются в точке K
, образуя угол AKD
, равный 30^{\circ}
. Найдите площадь треугольника AKD
, если площадь трапеции равна P
.
Ответ. \frac{3}{2}P
или \frac{1}{2}P
Указание. Докажите, что трапеция ABCD
— равнобедренная.
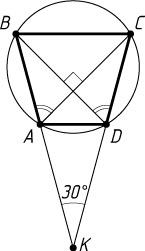
Решение. Пусть AD\gt BC
. Тогда точки K
и A
лежат по разные стороны от прямой BC
. Поскольку \angle BAC=\angle CDB
, то около трапеции ABCD
можно описать окружность. Поэтому трапеция — равнобедренная. Следовательно, треугольники AKD
и BKC
— также равнобедренные.
Поскольку
\angle BAC=\angle BAD-\angle CAD=75^{\circ}-45^{\circ}=30^{\circ},
то треугольник ACK
— равнобедренный, CK=AC
. Тогда
S_{\triangle BKC}=\frac{1}{2}CK^{2}\sin30^{\circ}=\frac{1}{4}CK^{2},
а так как
P=S_{ABCD}=\frac{1}{2}AC\cdot BD=\frac{1}{2}AC^{2}=\frac{1}{2}CK^{2},
то S_{\triangle BKC}=\frac{1}{2}P
. Следовательно,
S_{\triangle AKD}=\frac{1}{2}P+P=\frac{3}{2}P.
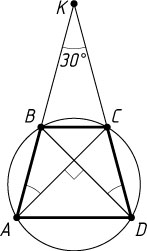
Если AD\lt BC
, то точки K
и A
лежат по одну сторону от прямой BC
. В этом случае, рассуждая аналогично, получим, что
S_{\triangle AKD}=\frac{1}{2}P.
Источник: Вступительный экзамен на географический факультет МГУ. — 1976, № 5, вариант 3
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.32, с. 32

