12459. В выпуклом четырёхугольнике ABCD
справедливы следующие соотношения: AB=BC
, AD=BD
и \angle ADB=2\angle BDC
. Известно, что \angle ACD=100^{\circ}
. Найдите \angle ADC
.
Ответ. 60^{\circ}
.
Указание. Отобразите точку C
относительно прямой BD
.
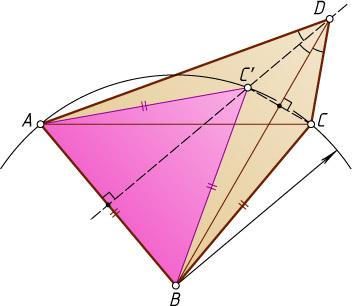
Решение. Пусть точка C'
симметрична точке C
относительно прямой BD
. Тогда BC'=BC
и \angle C'DB=\angle CDB
. Из симметрии и из условия \angle ADB=2\angle BDC
следует, что \angle C'DB=\frac{1}{2}\angle ADB
, поэтому точка C'
лежит на биссектрисе угла ADB
при вершине D
равнобедренного треугольника ADB
. Тогда прямая DC'
— серединный перпендикуляр к отрезку AB
, поэтому
C'A=C'B=BC=AB.
Значит, треугольник ABC'
равносторонний.
Точки A
, C
и C'
лежат на окружности с центром B
и радиусом BA
. Вписанный в эту окружность угол ACC'
равен половине соответствующего центрального угла ABC'
, т. е.
\angle ACC'=\frac{1}{2}\angle ABC'=30^{\circ}.
Значит,
\angle CC'D=\angle C'CD=\angle ACD-\angle ACC'=100^{\circ}-30^{\circ}=70^{\circ}.
Тогда
\angle CDB=\frac{1}{2}\angle CDC'=\frac{1}{2}(180^{\circ}-2\cdot70^{\circ})=20^{\circ}.
Следовательно,
\angle ADC=3\angle CDB=3\cdot20^{\circ}=60^{\circ}.
Автор: Кунгожин М. А.
Источник: Казахская республиканская олимпиада по математике. — 2014, задача 5, 9 класс
