1247. В трапеции ABCD
диагонали AC
и DB
взаимно перпендикулярны, \angle ABD=\angle ACD
. На продолжениях боковых сторон AB
и DC
за большее основание AD
отложены отрезки AM
и DN
так, что получается новая трапеция MADN
, подобная трапеции ABCD
. Найдите площадь трапеции MBCN
, если площадь трапеции ABCD
равна P
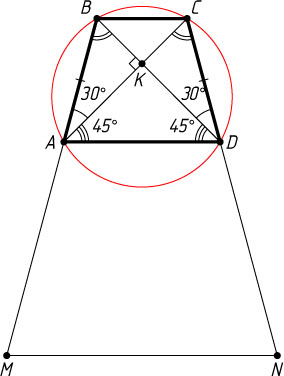
, а сумма углов при большем основании равна 150^{\circ}
.
Ответ. 4P
.
Указание. Докажите, что трапеция ABCD
— равнобедренная.
Решение. Пусть K
— точка пересечения диагоналей трапеции ABCD
. Поскольку \angle ABD=\angle ACD
, то около трапеции ABCD
можно описать окружность. Поэтому трапеция ABCD
— равнобедренная,
\angle BAK=\angle BAD-\angle KAD=75^{\circ}-45^{\circ}=30^{\circ}.
Следовательно,
\frac{AK}{KB}=\ctg30^{\circ}=\sqrt{3}.
Коэффициент подобия трапеций MADN
и ABCD
равен
\frac{AD}{BC}=\frac{AK}{KC}=\frac{AK}{KB}=\sqrt{3}.
Поэтому
S_{MADN}=(\sqrt{3})^{2}S_{ABCD}=3P.
Следовательно,
S_{MBCN}=S_{MADN}+S_{ABCD}=4P.
Источник: Вступительный экзамен на географический факультет МГУ. — 1976, № 5, вариант 2
