1250. Из одной точки окружности проведены две хорды, равные 9 и 17. Найдите радиус окружности, если расстояние между серединами данных хорд равно 5.
Ответ. \frac{85}{8}
.
Указание. Отрезок, соединяющий середины данных хорд, есть средняя линия треугольника с вершинами в концах этих хорд.
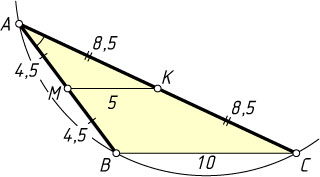
Решение. Пусть AB=9
и AC=17
— данные хорды, M
и K
— их середины. Поскольку MK
— средняя линия треугольника ABC
, то BC=10
.
По формуле Герона
S_{\triangle ABC}=\sqrt{18\cdot1\cdot9\cdot8}=9\cdot4=36.
С другой стороны,
S_{\triangle ABC}=\frac{1}{2}AB\cdot AC\sin\angle A=\frac{1}{2}\cdot9\cdot17\sin\angle A.
Отсюда находим, что \sin\angle A=\frac{8}{17}
. Следовательно, искомый радиус равен
\frac{BC}{2\sin\angle A}=\frac{10\cdot17}{2\cdot8}=\frac{85}{8}.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.203, с. 172
