12504. Даны две пересекающиеся окружности радиусов \sqrt{2}
и \sqrt{17}
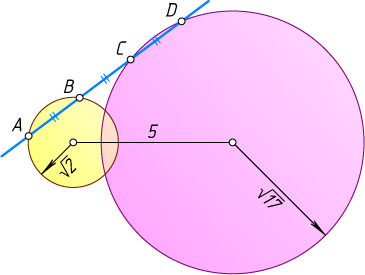
, расстояние между центрами которых равно 5. Прямая пересекает эти окружности в точках A
, B
, C
и D
так, как это показано на рисунке, причём отрезки AB
, BC
и CD
равны. Найдите эти отрезки.
Ответ. 2.
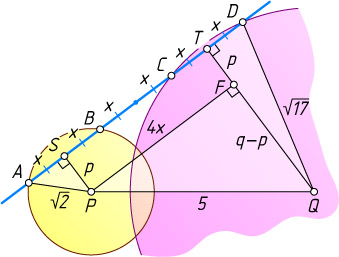
Решение. Пусть AB=BC=CD=2x
, а P
и Q
— центры окружностей. Опустим перпендикуляры PS=p
и QT=q
на прямую AB
. Тогда S
и T
— середины хорд AB
и CD
соответственно (см. задачу 1676). Опустим перпендикуляр PF
на прямую QT
. По теореме Пифагора из прямоугольных треугольников ASP
, DTQ
и PQF
получаем
x^{2}+p^{2}=2,~x^{2}+q^{2}=17,~16x^{2}+(q-p)^{2}=25,
или
16x^{2}+(\sqrt{17-x^{2}}-\sqrt{2-x^{2}})^{2}=25.
После очевидных упрощений получаем уравнение 48x^{4}-23x^{2}-25=0
, из которого находим, что
x^{2}=\frac{23\pm\sqrt{5329}}{96}=\frac{23\pm73}{96}=-\frac{25}{48},1.
Условию задачи удовлетворяет единственный положительный корень x=1
. Следовательно,
AB=BC=CD=2x=2.
Источник: Всесибирская физико-математическая олимпиада. — 2012, заключительный этап, задача 4, 11 класс

