1251. Из одной точки окружности проведены две хорды, равные 10 и 12. Найдите радиус окружности, если расстояние от середины меньшей хорды до большей равно 4.
Ответ. \frac{25}{4}
.
Указание. Соедините середины данных хорд.
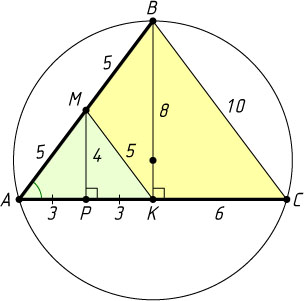
Решение. Пусть M
— середина хорды AB=10
, MP
— перпендикуляр, опущенный из точки M
на большую хорду AC=12
, K
— середина большей хорды. Тогда
AP=\sqrt{AM^{2}-MP^{2}}=\sqrt{5^{2}-4^{2}}=3,~PK=AK-AP=3.
Поэтому треугольник AMK
— равнобедренный.
Поскольку MK
— средняя линия треугольника ABC
, то
BC=2MK=10,~\sin\angle BAC=\frac{MP}{AM}=\frac{4}{5}.
Если R
— искомый радиус, то
R=\frac{BC}{2\sin\angle BAC}=\frac{10}{2\cdot\frac{4}{5}}=\frac{25}{4}.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.204, с. 172
