12585. На рисунке изображены два равных треугольника: ABC
и EBD
. Оказалось, что \angle DAE=\angle DEA=37^{\circ}
. Найдите угол BAC
.
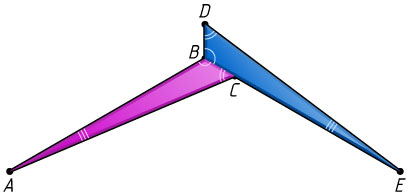
Ответ. 7^{\circ}
.
Решение. Проведём отрезки AD
и AE
. Поскольку \angle DAE=\angle DEA=37^{\circ}
, треугольник ADE
равнобедренный, AD=DE
.
Треугольник ABD
равен треугольнику EBD
по трём сторонам (BD
— общая сторона, AD=DE
и AB=BE
из равенства треугольников ABC
и EBD
). Тогда
\angle DAB=\angle BED=\angle BAC,
\angle ABD=\angle DBE=\angle ABE=\frac{1}{3}\cdot360^{\circ}=120^{\circ}.
Поскольку AB=BE
, треугольник ABE
равнобедренный с углом 120^{\circ}
при вершине B
. Значит, \angle BAE=30^{\circ}
. Следовательно,
\angle BAC=\angle DAB=\angle DAE-\angle BAE=37^{\circ}-30^{\circ}=7^{\circ}.
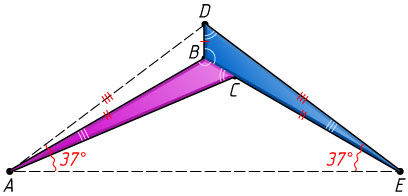
Источник: Всероссийская олимпиада школьников. — 2021-2022, XLVIII, школьный этап, задача 7, 8 класс

