12588. На окружности по часовой стрелке расположены точки A
, B
, C
, D
, E
, F
, G
, как изображено на рисунке. Известно, что AE
— диаметр окружности. Также известно, что \angle ABF=81^{\circ}
, \angle EDG=76^{\circ}
. Сколько градусов составляет угол FCG
?
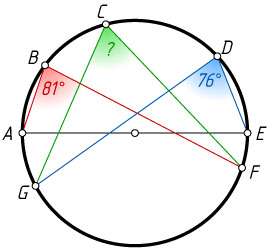
Ответ. 67^{\circ}
.
Решение. Вписанные углы, опирающиеся на одну и ту же дугу, равны, поэтому
\angle ACF=\angle ADF=81^{\circ},~\angle ECG=\angle EDG=76^{\circ}.
Точка C
лежит на окружности с диаметром AE
, поэтому \angle ACE=90^{\circ}
, а так как
\angle ACE=\angle ACF+\angle ECG-\angle FCG,
то
\angle FCG=\angle ACF+\angle ECG-\angle ACE=81^{\circ}+76^{\circ}-90^{\circ}=67^{\circ}.
Источник: Всероссийская олимпиада школьников. — 2021-2022, XLVIII, школьный этап, задача 2, 10 класс
