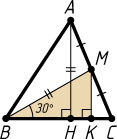
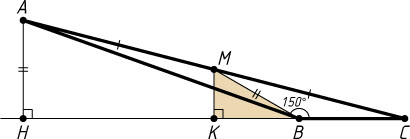
1259. В треугольнике ABC
проведены медиана BM
и высота AH
. Известно, что BM=AH
. Найдите угол MBC
.
Ответ. 30^{\circ}
или 150^{\circ}
.
Указание. Опустите перпендикуляр из точки M
на прямую BC
.
Решение. Опустим из точки M
перпендикуляр MK
на прямую BC
. Тогда MK
— средняя линия треугольника AHC
. Поэтому
MK=\frac{1}{2}AH=\frac{1}{2}BM.
Тогда
\sin\angle MBC=\frac{MK}{MB}=\frac{1}{2}.
Следовательно, угол MBC
равен 30^{\circ}
или 150^{\circ}
.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 61, с. 196
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 12.54, с. 293

