12590. Квадрат разрезали на пять прямоугольников равной площади, как изображено на рисунке. Ширина одного из прямоугольников равна 5. Найдите площадь квадрата.
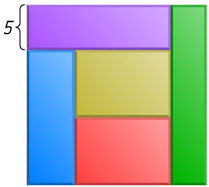
Ответ. 400.
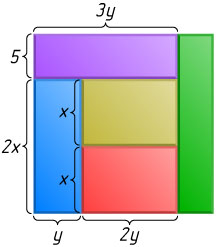
Решение. У центрального прямоугольника и у прямоугольника под ним есть общая горизонтальная сторона, а площади их равны. Значит, вертикальные стороны этих прямоугольников равны, обозначим их через x
. У левого нижнего прямоугольника вертикальная сторона равна 2x
, его горизонтальную сторону обозначим через y
. Поскольку его площадь 2xy
совпадает с площадью центрального прямоугольника, то горизонтальная сторона центрального прямоугольника равна 2y
. Тогда горизонтальная сторона левого верхнего прямоугольника равна 3y
, и его площадь 3y\cdot5=15y
должна быть равна 2xy
. Из равенства 15y=2xy
находим, что x=7{,}5
. Тогда у всего квадрата сторона равна
5+2x=5+2\cdot7{,}5=20,
а его площадь равна 20^{2}=400
.
Источник: Всероссийская олимпиада школьников. — 2021-2022, XLVIII, школьный этап, задача 2, 11 класс

