12609. Сравните углы BAC
и CED
(см. рисунок). Свой ответ обоснуйте.
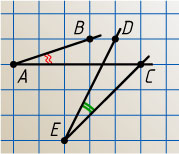
Ответ. Эти углы равны.
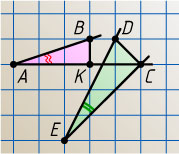
Решение. Пусть K
— основание перпендикуляра, опущенного из точки B
на AC
. Рассмотрим треугольники ABK
и EDC
. Они оба прямоугольные, причём их катеты относятся как 1:3
. Значит, треугольники подобны, поэтому их соответствующие острые углы равны. Следовательно,
\angle BAC=\angle BAK=\angle DEC.
Источник: Всероссийская олимпиада школьников. — 2017-2018, XLIV, школьный этап, задача 4, 10 класс

