1261. В выпуклом четырёхугольнике прямая, проходящая через середины двух противоположных сторон, образует равные углы с диагоналями четырёхугольника. Докажите, что диагонали равны.
Указание. Соедините указанные середины сторон с серединой третьей стороны четырёхугольника.
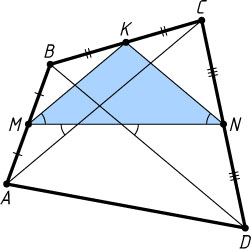
Решение. Пусть M
, N
и K
— середины сторон AB
, CD
и BC
четырёхугольника ABCD
, причём прямая MN
образует равные углы с диагоналями.
Поскольку MK
и KN
— средние линии треугольников ABC
и BCD
, то \angle KMN=\angle KNM
. Поэтому треугольник MKN
— равнобедренный, KM=KN
. Следовательно, AC=BD
.
Примечание. Верно и обратное утверждение, если диагонали четырёхугольника равны, то прямая, проходящая через середины противоположных сторон, образует с диагоналями равные углы. Доказательство аналогично приведённому.
Автор: Анджанс А. В.
Источник: Всесоюзная олимпиада по математике. — 1990, XXIV
