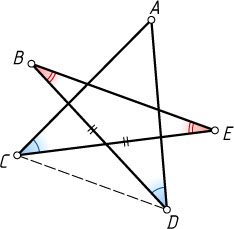
12612. В пятиугольной звезде, изображённой на рисунке, \angle ACE=\angle ADB
и \angle DBE=\angle BEC
. Известно также, что BD=CE
. Докажите, что \angle ACD=\angle ADC
.
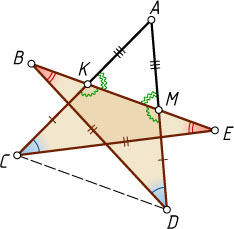
Решение. Пусть отрезки AC
и AD
пересекают отрезок BE
в точках K
и M
соответственно. Из условия задачи следует, что треугольники CEK
и DBM
равны по стороне и двум прилежащим к ней углам. Следовательно,
CK=DM~\mbox{и}~\angle CKE=\angle DMB.
Тогда \angle AKE=\angle AMB
как углы, смежные с равными.
В треугольнике AMK
равны углы, прилежащие к стороне MK
, поэтому этот треугольник равнобедренный (AK=AM
). Следовательно,
AC=AK+CK=AM+DM=AD,
значит, треугольник ACD
тоже равнобедренный (с основанием CD
), поэтому \angle ACD=\angle ADC
. Что и требовалось доказать.
Источник: Всероссийская олимпиада школьников. — 2012-2013, XXXIX, школьный этап, задача 4, 8 класс

