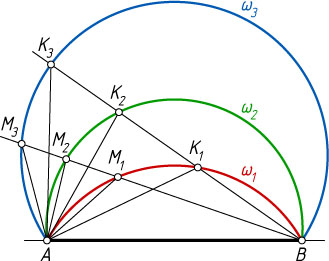
12637. Три дуги окружностей \omega_{1}
, \omega_{2}
, \omega_{2}
с общей хордой AB
расположены по одну сторону от прямой AB
, причём дуга окружности \omega_{2}
между дугами окружностей \omega_{1}
и \omega_{3}
(см. рисунок). Два луча с началом в точке B
пересекают эти дуги: первый — в точках M_{1}
, M_{2}
, M_{3}
соответственно, второй — в точках K_{1}
, K_{2}
, K_{3}
соответственно. Докажите, что \frac{M_{1}M_{2}}{M_{2}M_{3}}=\frac{K_{1}K_{2}}{K_{2}K_{3}}
.
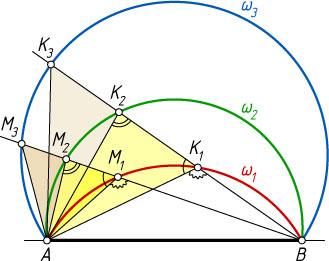
Решение. Заметим, что \angle AK_{1}B=\angle AM_{1}B
и \angle AK_{2}B=\angle AM_{2}B
по теореме о вписанных углах. Тогда
\angle AK_{1}K_{2}=\angle180^{\circ}-\angle AK_{1}B=180^{\circ}-\angle AM_{1}B=\angle AM_{1}M_{2}.
Значит, треугольники AK_{1}K_{2}
и AM_{1}M_{2}
подобны по двум углам. Тогда \frac{K_{1}K_{2}}{M_{1}M_{2}}=\frac{AK_{2}}{AM_{2}}
. Аналогично, из подобия треугольников AK_{2}K_{3}
и AM_{2}M_{3}
получаем \frac{K_{2}K_{3}}{M_{2}M_{3}}=\frac{AK_{2}}{AM_{2}}
. Следовательно, \frac{K_{1}K_{2}}{M_{1}M_{2}}=\frac{K_{2}K_{3}}{M_{2}M_{3}}
, откуда \frac{M_{1}M_{2}}{M_{2}M_{3}}=\frac{K_{1}K_{2}}{K_{2}K_{3}}
. Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2009, № 3, задача 20, с. 159
Источник: Олимпиада «Baltic Way». — 2004, задача 20

