1264. Точка пересечения медиан прямоугольного треугольника удалена от катетов на расстояния 3 и 4. Найдите расстояние от этой точки до гипотенузы.
Ответ. \frac{12}{5}
.
Указание. Учитывая, что медианы треугольника делятся точкой их пересечения в отношении 2:1
, найдите катеты треугольника.
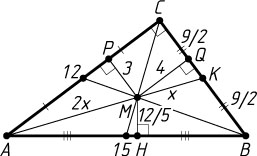
Решение. Первый способ. Пусть M
— точка пересечения медиан прямоугольного треугольника ABC
с катетами AC
и BC
, P
и Q
— проекции точки M
на AC
и BC
соответственно, MP=3
, MQ=4
, K
— середина BC
.
Поскольку медианы треугольника делятся точкой пересечения в отношении 2:1
, считая от вершины треугольника, то
\frac{AC}{PC}=\frac{AK}{MK}=3.
Поэтому
AC=3PC=3MQ=12.
Аналогично BC=9
. Тогда AB=15
.
S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=54.
С другой стороны,
S_{\triangle ABC}=S_{\triangle AMC}+S_{\triangle BMC}+S_{\triangle AMB}=
=\frac{1}{2}AC\cdot MP+\frac{1}{2}BC\cdot MQ+\frac{1}{2}AB\cdot x=18+18+\frac{15\cdot x}{2},
где x
— искомое расстояние. Следовательно,
x=\frac{2(54-36)}{15}=\frac{12}{5}.
Второй способ. Пусть M
— точка пересечения медиан прямоугольного треугольника ABC
с катетами AC
и BC
, P
и Q
— проекции точки M
на AC
и BC
соответственно, MP=3
, MQ=4
, K
— середина BC
.
Поскольку медианы треугольника делятся точкой пересечения в отношении 2:1
, считая от вершины треугольника, то
\frac{AC}{PC}=\frac{AK}{MK}=3.
Поэтому
AC=3PC=3MQ=12.
Аналогично BC=9
. Тогда AB=15
.
Пусть h
— высота треугольника ABC
, проведённая из вершины прямого угла, H
— проекция точки M
на AB
. Поскольку
h=\frac{AC\cdot BC}{AB}=\frac{9\cdot12}{15}=\frac{36}{5},
то MH=\frac{1}{3}h=\frac{12}{5}
.
Источник: Вступительный экзамен в МАТИ. — № 5, 1989
Источник: Журнал «Квант». — 1990, № 5, с. 68
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 5.28, с. 50
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 5.28.1, с. 50
