12645. Медианы треугольника ABC
пересекаются в точке M
. Прямая t
, проходящая через точку M
, пересекает описанную окружность треугольника ABC
в точках X
и Y
, причём точки A
и C
лежат по одну сторону от прямой t
. Докажите, что BX\cdot BY=AX\cdot AY+CX\cdot CY
.
Решение. Лемма. Если диагонали вписанного четырёхугольника ABCD
пересекаются в точке O
, то \frac{AB\cdot BC}{AD\cdot DC}=\frac{BO}{OD}
.
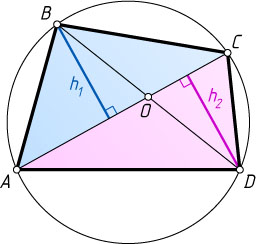
Доказательство. Четырёхугольник ABCD
вписанный (рис. 1), поэтому \angle ADC=180^{\circ}-\angle ABC
. Значит, \sin\angle ADC=\sin\angle ABC
. Пусть h_{1}
и h_{2}
— высоты треугольников ABC
и ADC
, проведённые из вершин B
и D
соответственно. Тогда
\frac{AB\cdot BC}{AD\cdot DC}=\frac{\frac{1}{2}AB\cdot BC\sin\angle ABC}{\frac{1}{2}AD\cdot DC\sin\angle ADC}=\frac{S_{\triangle ABC}}{S_{\triangle ADC}}=\frac{\frac{1}{2}AC\cdot h_{1}}{\frac{1}{2}AC\cdot h_{2}}=\frac{h_{1}}{h_{2}}=\frac{BO}{OD}.
Лемма доказана.
Пусть прямая XY
пересекает стороны AB
и BC
треугольника ABC
в точках R
и S
соответственно, причём точки X
, R
, S
и Y
расположены на этой прямой в указанном порядке. Применив доказанную лемму к вписанным четырёхугольникам AXBY
и CXBY
, получим
\frac{AX\cdot AY}{BX\cdot BY}=\frac{AR}{RB}~\mbox{и}~\frac{CX\cdot CY}{BX\cdot BY}=\frac{CS}{SB}.
Тогда
\frac{AR}{RB}+\frac{CS}{SB}=\frac{AX\cdot AY}{BX\cdot BY}+\frac{CX\cdot CY}{BX\cdot BY}=\frac{AX\cdot AY+CX\cdot CY}{BX\cdot BY},
поэтому достаточно доказать равенство
\frac{AR}{RB}+\frac{CS}{SB}=1.
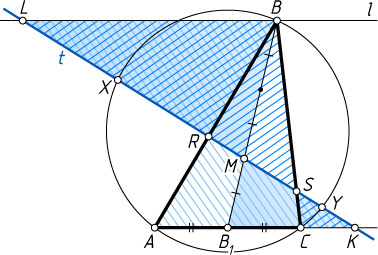
Через вершину B
проведём прямую l
, параллельную стороне AC
(рис. 2). Пусть прямая RS
пересекает прямую l
в точке L
, прямую AC
— в точке K
, а BB_{1}
— медиана треугольника ABC
. Треугольник KAR
подобен треугольнику LBR
, треугольник BSL
— треугольнику CSK
, а треугольник BML
— треугольнику B_{1}MK
(с коэффициентом \frac{BM}{MB_{1}}=2
), поэтому
\frac{AR}{RB}=\frac{AK}{BL},~\frac{CS}{SB}=\frac{CK}{BL},~BL=2KB_{1}=2CK+2CB_{1}=
=CK+(CK+2CB_{1})=CK+AK.
Значит,
\frac{AR}{RB}+\frac{CS}{SB}=\frac{AK}{BL}+\frac{CK}{BL}=\frac{AK+CK}{BL}=\frac{AK+CK}{AK+CK}=1.
Отсюда следует утверждение задачи.
Если SR\parallel AC
, решение очевидно.
Источник: Олимпиада «Baltic Way». — 2006, задача 15

