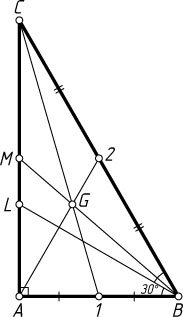
1266. В треугольнике ABC
угол BAC
прямой, стороны AB
и BC
равны соответственно 1 и 2. Биссектриса угла ABC
пересекает сторону AC
в точке L
, G
— точка пересечения медиан треугольника ABC
. Что больше, BL
или BG
?
Ответ. BL\gt BG
.
Указание. Отрезок BG
составляет \frac{2}{3}
медианы треугольника ABC
, проведённой из вершины B
.
Решение. Поскольку BC=2AB
, то
\angle ABC=60^{\circ},~\angle ABL=30^{\circ}.
Поэтому
BL=\frac{AB}{\cos30^{\circ}}=\frac{2}{\sqrt{3}}=\frac{2\sqrt{3}}{3}.
Пусть M
— середина катета AC
. Тогда
AM=\frac{1}{2}AC=\frac{\sqrt{3}}{2},
BG=\frac{2}{3}\cdot BM=\frac{2}{3}\sqrt{AB^{2}+AM^{2}}=\frac{\sqrt{7}}{3}.
Поскольку \frac{2\sqrt{3}}{3}\gt\frac{\sqrt{7}}{3}
, то BL\gt BG
.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1983 (отделение геофизики), вариант 1, № 2
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 83
