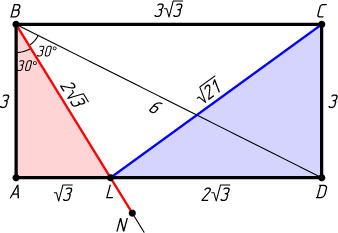
1267. В прямоугольнике ABCD
отрезки AB
и BD
равны соответственно 3 и 6. На продолжении биссектрисы BL
треугольника ABD
взята точка N
, причём точка L
делит отрезок BN
в отношении 10:3
, считая от точки B
. Что больше: BN
или CL
?
Ответ. BN\lt CL
.
Указание. Найдите указанные отрезки из соответствующих прямоугольных треугольников.
Решение. Поскольку BD=2AB
, то
\angle ABD=60^{\circ},~\angle ABL=30^{\circ}.
Поэтому
BL=\frac{AB}{\cos30^{\circ}}=2\sqrt{3},~BN=\frac{13}{10}BL=\frac{13\sqrt{3}}{5}.
AD=AB\tg60^{\circ}=3\sqrt{3},~AL=AB\tg30^{\circ}=\sqrt{3},
DL=AD-AL=2\sqrt{3},~CL=\sqrt{DC^{2}+DL^{2}}=\sqrt{9+12}=\sqrt{21}.
Поскольку \frac{13\sqrt{3}}{5}\lt\sqrt{21}
, то BN\lt CL
.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1983 (отделение геофизики), вариант 2, № 2
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 84
